Card Counting the King’s Bounty Blackjack Side Bet: 6 Decks
King’s Bounty (KB) is Bally’s answer to Galaxy Gaming’s Lucky Ladies (LL) blackjack side bet. Both wagers pay based on the player’s two cards totaling 20. Both side bets have a special payout for a matched pair. In LL, this pair consists of two Queen of Hearts. In KB, this pair consists of two King of Spades. Both games have a top prize of 1000-to-1 that is paid when the premium pair occurs simultaneously with a dealer blackjack. I have always assumed that KB and LL have about the same vulnerability to card counting, with the Ten count working for both.
The most significant difference between the two wagers is that KB is not available for two decks. Only one pay table is given in the documentation I found online.18 This pay table gives a house edge over the statutory maximum of 25% for two decks. Without evidence of a pay table suitable for two decks, I must conclude the game was not designed to be used in this situation. For this reason, the present analysis is limited to the six-deck version of KB.
The payouts for winning KB bets are as follows. Only the highest payout is paid:
- Pair of King of Spades with dealer blackjack pays 1000-to-1.
- Pair of King of Spades without dealer blackjack pays 100-to-1.
- Two suited Kings pays 30-to-1.
- Two suited Queens, Jacks or Tens pays 20-to-1.
- A suited total of 20 pays 9-to-1.
- Two unsuited Kings pays 6-to-1.
- An unsuited total of 20 pays 4-to-1.
- Otherwise, the player loses the KB bet.
The following table gives the combinatorial analysis for the KB bet for 6 decks:
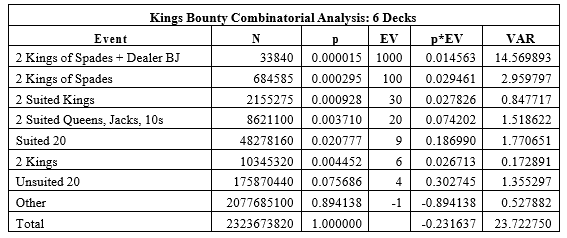
In particular, note that:
- The house edge for the six-deck version is 23.164%.
- The hit frequency for the six-deck version is 10.586%.
- The standard deviation for the six-deck version is 4.871.
By comparison, the house edge for the six-deck version of LL is 24.709%. The house edge for KB is about 1.5% less than LL. It follows that KB should be slightly more vulnerable to card counting than the six-deck version of LL. As we will see, this is the case.
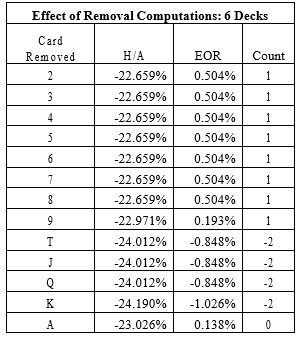
I computed the EORs for KB to see if a card counting system based around Kings was possible. The following table shows that Kings are slightly more important than other ten-valued cards, but this significance is not enough to generate a different counting tag for all Kings. The betting correlation for the Ten count is a very strong 0.987.
Here are the results of a simulation of one hundred million (100,000,000) six-deck shoes of KB, using the Ten count:
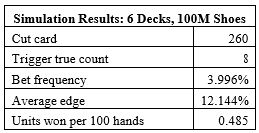
If the maximum bet is $100, and the AP is playing heads-up, getting 200 rounds per hour, then the AP using the Ten count on a six-deck shoe game will earn about $97.04 per hour from KB. By comparison, as shown in Chapter 27, the AP using the Ten count against LL will earn $79.78 per hour. As expected, KB is slightly more vulnerable to card counting than LL.
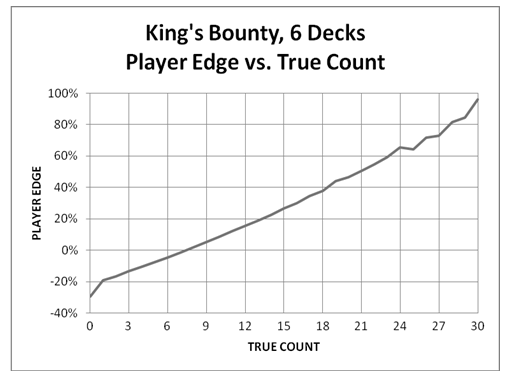
The following graph shows the potential edge the AP can get over the house against KB using the Ten count. The edges that are possible for the AP at high true counts are impressive:
A separate tag for the King of Spades can be used to strengthen this count, similar to the tag of -6 used for Queen of Hearts in the six-deck version of LL. This modification gives the Optimal KB count. The Optimal KB count has the following tags:
- A, 2, 3, 4, 5, 6, 7, 8, 9 = +1.
- T,J,Q = -2.
- King, not spades = -2.
- King of spades = -6.
Here are the results of a simulation of one hundred million (100,000,000) six-deck shoes of KB, using the Optimal KB count:
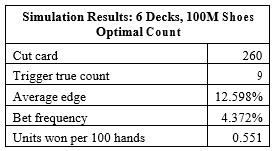
The Optimal KB count returns 0.551 units per 100 hands, compared to a return of 0.485 units per 100 hands using the Ten count. The Optimal count returns 13.6% more than the Ten count.
Clearly, KB can also be attacked in the six-deck version by shuffle tracking or any other method that allows the AP to keep track of a group of ten-valued cards.
